Fungicide application, while helpful in controlling plant diseases, has complicated limitations that may cost growers both peace of mind and quantity of yield. Plant pathogens which would otherwise be killed off by fungicides can evolve to avenge their dead siblings, developing resistance that renders the standard dose of fungicide application ineffective.
To delay fungicide resistance, growers commonly use mixtures of fungicides to treat yield-limiting fungal diseases—based on extensive research outlining how to construct these mixtures. However, this research does not completely translate to the common, real-world scenario where one fungicide has been available longer than the other, begging the question: what is the optimal strategy for application of fungicide mixtures when the initial levels of resistance to each fungicide differ?
To address this question, Nick Taylor and Nik Cunniffe from the University of Cambridge in the United Kingdom constructed a simple, alternative strategy by analyzing a mathematical model that incorporates pathogen sexual reproduction, which rarely is included in modeling studies despite its relevance to the evolutionary dynamics of fungal pathogens.
Their paper, recently published in Phytopathology, applies the model to an economically important disease, Septoria leaf blotch on wheat, and provides an extensive analysis of its evolutionary dynamics.
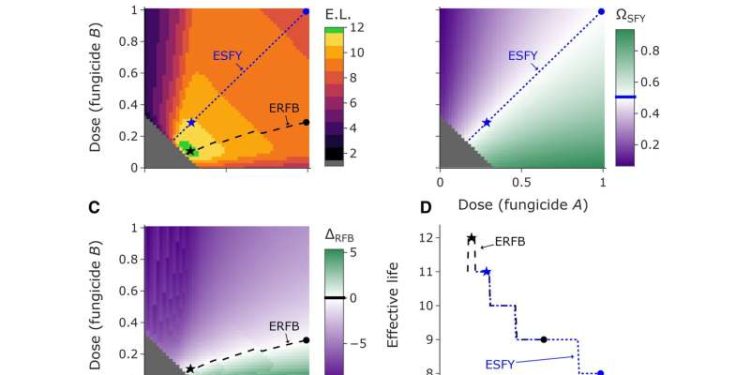
Taylor and Cunniffe use the theoretical and mathematical model to find the optimal disease management strategy when initial resistance frequencies to the two fungicides in the mixture differ. The model demonstrates that previous modeling recommendations for fungicide resistance management are suboptimal and may fail in varying real-world circumstances.
In contrast, their novel strategy is optimal even when initial resistance frequencies differ and when fungicide parameters and the proportion of between-season pathogen sexual reproduction varies. Additionally, they find that between-season pathogen sexual reproduction can affect the rate of resistance development but does not qualitatively affect the optimal strategy recommendation.
While this may seem complicated, Taylor comments, “The most exciting aspect of this research is the idea that such a complex problem can have a very simple solution. Although managing pathogen resistance to mixtures containing pairs of fungicides to which pathogens can potentially acquire resistance is difficult and complex, the optimal management strategy reliably works and is simple to state: the fungicide application program should be designed so that resistance to both fungicides is balanced by the end of the program.”
Ultimately, their strategy aims to balance disease control with resistance management by balancing resistance to both fungicides until resistance has increased so much that the program fails.
This strategy recommendation is robust to variations in parameters controlling pathogen epidemiology and fungicide efficacy, and once this strategy is verified experimentally in the future, it could potentially influence policy recommendations surrounding effective agricultural disease management. Cunniffe looks forward to “extending these ideas to allow for more complex models including fungicide resistance, as well as for resistance management strategies that vary over time.”